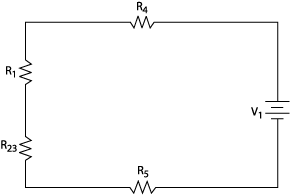
Q2: Draw a simplified circuit with only ONE series resistor

 

Q3: Find the total equivalent resistance for all resistors in this circuit.

Total Resistance is 56.7W R₂ and R₃ are parallel and must be added first. Let R₂₃ equal R₂ and R₃ added together

 

1/R₂₃ = 1/R₂ + 1/R₃

1/R₂₃ = 1/20.0 W + 1/10.0 W

1/R₂₃ = 3/20 W

1/R₂₃ = .15 1/W

R₂₃= 6.7 W

Replacing R₂₃ for R₂ and R₃ we can now add all resistors in series.

R₁ + R₂₃+ R₄ + R₅ = Total Resistance

20.0 W + 6.7 W + 20.0 W + 10.0 W = 56.7 W

Total Resistance = 56.7 W

.

Q4: What current flows through the battery?

Total current through the battery is 0.18 A. [1 pt]

.

V = IR

.

10 V = I (56.7 W)

.

I = 10 V/56.7 W

.

I = 0.176 A

Q5: What current flows through each resistor?

R₁, R₂₃, R₄, and R₅, all have 0.18 A of current.

For R₁, R₄, and R₅

I(R₁) = I(T) = 0.176 A

R₂ and R₃ must be found individually using the Voltage drop across _R23:

 

V₂₃ = I₂₃ * R₂₃

V₂₃ = 0.176 A (6.7 W)

V₂₃ = 1.18 V

This voltage drop is the same for R₂ and R₃, therefore:

V₂₃ = I₂ * R₂

1.18 V = I₂ * 20.0W

I₂ = 0.059 A

V₂₃ = I₃ * R₃

1.18V = I₃ * 10.0W

I₃ = 0.118 A

Q6: What is the potential difference (voltage drop) across each resistor?

Voltage drop for each resistor must equal total voltage drop for entire system, which is 10.0 V.

For R₁, and R₄ V = IR

V = 0.176 A * 20.0W

V = 3.52 V

For R₅, V = IR

V = 0.176 A * 10.0 W

V = 1.76 V

For R₂₃, V = IR

V = 0.176 A * 6.7W

V = 1.18 V

Because R₂ and R₃ are in parallel you must use their combined resistance to find the voltage drop over each individual resistor.

 

For R₂, V = IR V = 0.059 V

 

A * 6.7W = 0.40 V

For R₃, V = IR

V = 0.118 A * 6.7 W

V = 0.80 V

All voltages add up to the total voltage drop across the battery.

 

3.52 V + 3.52 V + 1.76V + 0.40 V + 0.80 V = 10.0 V