Magnetism
Motion of Charged Particles in Magnetic Fields
Solutions

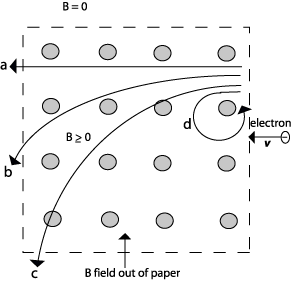
Q1: On your whiteboard, make four illustrations of the electrons' path inside the dotted region, one for each of the following field strengths:

(a) B = 0 inside the region marked by the dotted-line
(b) weak B field inside the region marked by the dotted-line
(c) medium strength B field inside the region marked by the dotted-line
(d) very strong B field inside the region marked by the dotted-line

 

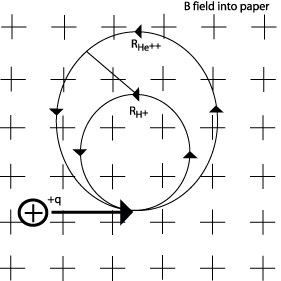
An electron with velocity pointed toward the left side of the page is analogous to a positive charge moving in toward the right side of this page.  Using RHR #1 the electron feels a force pushing it down.

Q2: On your whiteboard, calculate the relative sizes of the two circular paths and sketch them to scale showing the direction of travel for each.  Recall equations for centripetal acceleration and force.  Give explanations for your reasoning.

Using RHR #1, the direction of the of the force due to the magnetic field is upwards:A hydrogen ion is a proton so, qH+= +e and mH+ = mass of 1 proton. An alpha particle is a helium nucleus so, qHe++ = +2e and mHe++ = 4mH+. Recall that Fcentripetal= (mv2)/ r; where the direction of F is perpendicular to v, and Fmagnetic= qvB; where the direction of B is perpendicular to v.  Using this, (mv2)/ r = qvB (mv2)/ (qvB) = r = mv/ qB.rH+ = MV/ qB and rHe++ = 4mv/ 2qB; the radius of the He++ circular trajectory is twice as large as the radius of the H+ circular trajectory.

Seat Activities
Activity
Contributors