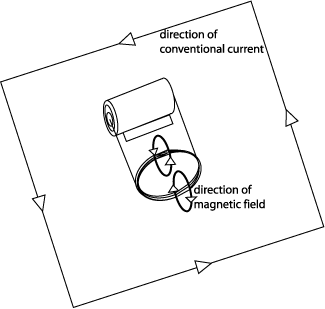
Q1: My motor armature had a resistance of 0.015 ohms. Assuming the 1.5V battery could drive a constant current through this coil at rest, what would the current be?

V/R = 1.5V/.015 W = 100 A

Q2: What would the electric power driven through the (stationary) coil be in watts?

P=IV = 100A x 1.5V = 150 Watts

Q3: Where would this energy go?

The energy is primarily consumed in raising the temperature of the copper coil.

Q4: An actual measured current flow through the coil is about 5 A. What magnetic field does this produce in an ideal coil? Draw the direction of this field in a diagram showing the coil.

B= Nm _oI/2R = N(4p x 10^-7)(5 A)] / (2 x R) For coils used in this experiment N» 10 R » .0175 m; B » 2 x 10^-4 Tesla

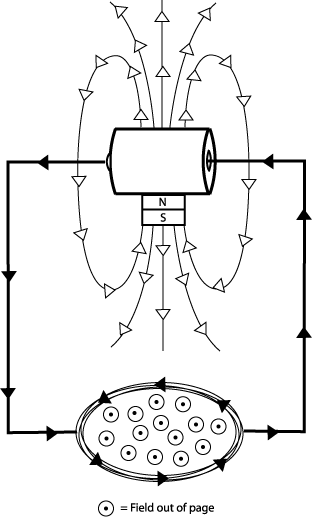
Q5: Why is the permanent magnet stuck to the D cell needed in our motor?

The permanent magnet provides an external field for the field produced by the coil to oppose. It is the interaction of the two fields that exerts a torque on the coil.

Q6: Sketch and describe the magnetic fields in this motor, including how they change direction.

Q7: View the motor in the dark. What do you see at the paper clip/armature connections? Why?

It is possible to see a small arc between the paper clip and armature. This is evidence that current is flowing through the coil.

Q8: An engineer could claim that this motor should simply lock itself into a single position, and the motor does have a tendency to do so. What is this (electrically powered) position? Why does it not continuously lock in this position?

This position is when the coil is perpendicular to the field of the permanent magnet such that the two fields are parallel and in the same direction. If the current through the coil was constant, any displacement from this position would result in a field interaction creating a torque that would tend to oppose the motion of the coil. These motors do not lock in this position because the enamel insulation is removed form only on half of the armature. When the motor reaches this position the current is interrupted and the coil rotates through the second half of its cycle due to its rotational inertia.

 Q9: A second magnet can be brought beneath the coil and can either slow or accelerate the armature's rotation (see below). Explain why, using a diagram.