Q1: A squirrel in the woods runs 2.0 m/s to the safety of a tree, trying to escape a coyote running at 4.0 m/s. If the coyote and squirrel start running when the coyote is 30 m away, what is the maximum safe distance the squirrel can be from the tree to avoid becoming lunch? Sketch and solve.

If we reflect on this problem for a moment we will realize that both the squirrel and the coyote run for exactly the same length of time. So time is common. Since we are given a speed (4m/s and 2m/s) and since we need time and distance, we can use the equation: V= d/t   so, d=Vt

Notice how I am finding the distance separating the two?

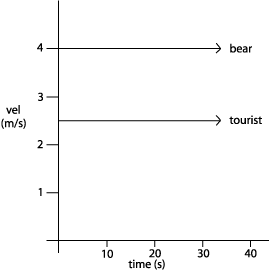
I can rewrite my expression and get this:

-4t + 2t + 30 = 0

-4t + 2t = -30    and now I can solve for t, time:

-2t = -30

t= 15 seconds, meaning that at 15 seconds the squirrel and the coyote are 0 meters apart.

So, how far can the squirrel run in 15 seconds?

V = d/t   --->   Vt = d     (2 m/s) x 15 s = d    d = 30 meters

Therefore the squirrel must be less than 15 seconds (30 meters) from a tree.

Q2: A tourist in Yosemite runs 2.5 m/s to the safety of his car, trying to escape a grizzly bear running at 4.0 m/s. The bear starts chasing the tourist from 50m away. What is the maximum safe distance the tourist can be away from his car to escape becoming an unfortunate statistic? Sketch and solve.

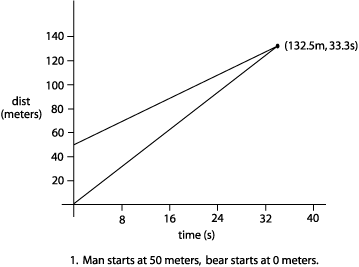
This problem is identical to the first problem, so I could just change the numbers and solve for the time.

Let's assume that the bear, man, and car are on an x-axis, with the bear at x = 0 meters, and the man at x = 50 meters.

Now I have:

So the distance the man is from the bear is: (2.5 t + 50) meters.

Now I can do as I previously did.

(Distance covered by bear) - (distance covered by man) = 0    (0 is when they meet)

and using V = d/t   or d = Vt   I get:  4.0 m/s x t - (2.5 m/s x t + 50) = 0    or,

4t - 2.5t - 50 = 0

4t - 2.5t = 50

1.5t = 50

t = 33.33 seconds   call it 33 seconds

Since the man can run at 2.5 m/s,  using d = Vt

The maximum distance the man can be is: d = (2.5)(33) = 82.5 meters from his car.

Q3: Plot distance and velocity for situation #2.

First velocity: For both man and bear, velocity is constant.

Q4: Develop a general algebraic expression (a formula) for situations of this sort: one object overtaking another, each with different velocities V_a and V_b, starting a distance s apart. Your formula needs to predict the distance d covered by the overtaken object when it is caught. Write your formula and describe it in two sentences.

V_a = velocity of overtaking object, V_b = velocity of overtaken object, t = time

V_at - (V_bt + s) = 0

V_at - V_bt - s = 0

V_at - V_bt = s

(V_a - V_b)t = s

t = s/(V_a - V_b)

d of overtaken = V_at = V_b[s/(V_a - V_b)]

The maximum distance that can be covered before being overtaken can be found by assuming the overtaken object to be at 0 meters and then multiplying the slower object's velocity by the ratio, initial separation distance over the distance in velocity. Note: The ratio must be a positive value.