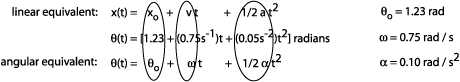|
|
|
|
| Solution |
|
Q1: How large are these angles in radians? A half rotation, a full rotation, 5 rotations, 45 degrees, 90 degrees, 360degrees. Half rotation (180°): 180° x 2p rad / 360° = p rad Full rotation (360°): 360° x 2p rad / 360° = 2p rad 5 rotations (5x360°): 1800° x 2p rad / 360° = 10p rad 45 degrees: 45° x 2p rad / 360° = p rad / 4 90 degrees: 90° x 2p rad / 360° = p rad / 2 360 degrees: 360° x 2p rad / 360° = 2p rad Q2: A car engine rotates at a rate of 4500 rpm (revolutions per minute). What is the angular velocity of the engine in radians / sec?
Q3: A man of height 180 cm subtends an angle of .0036 radians. How far away is the man? To solve this problem we must employ the equation: q = s / r
r = s / q = 1.8m / 0.0036 rad = 500 m The angular position of a merry-go-round after a switch is thrown is specified as: Q4: What are the inital angular position, angular velocity and angular acceleration of the merry-go-round before the switch is thrown? (Hint: compare to the linear kinematic equations.)
Q5: What are the angular position, velocity and acceleration of the merry-go-round at t = 5 seconds. a) Angular position: q (5s) = [1.23 rad + (0.75 rad / s)(5s) + 1/2(0.10 rad / s2)(5s)2] q (5s) = 1.23 rad + 3.75 rad + 1.25 rad = 6.23 rad b) Angular velocity: w = wo + a t, which is related to the linear equation v = vo + at w = 0.75 rad / s + (0.10 rad / s2 x 5s) = 1.25 rad / s c) Angular acceleration: remains constant at 0.10 rad / s2 An elecrical motor running at 1000 rpm is turned off, and its angular velocity decreases uniformly to 500 rpm over three seconds.Q6: What is the angular acceleration of the motor? To solve this problem, we can rearrange the equation w = wo + at to solve for a. However, we must first convert the angular velocities into rad/s as follows:
Now, rearranging w = wo + a t to solve for a, we get: a = (w - wo) / t a = (16.7p rad / s - 33.3p rad / s) / 3s = -5.5p rad / s2 (The negative sign indicates that the motor is slowing down. Q7: If the motor continues to decelerate uniformly from 500 to 0 rpm, how many revolutions does the motor turn through before coming to a rest? To solve this problem, we must employ the equation q(t) = qo + wt + 1/2a t2 as follows: q(3s) = 0 rad + (16.7 rad / s)(3s) + 1/2(-5.5p rad / s2)(3s)2 q(3s) = 50.1 rad - 24.75p rad = 25.35 p rad = 12.7 revolutions Q8: If the motor continues to uniformly coast to a halt, how much time is required to come to a complete stop? This question can be answered intuitively. If we know that the motor is decelerating uniformly, and it took 3 seconds to go from 1000 rpm to 500 rpm, then we know that it will take an additional 3 seconds to reach a halt. |
| References |
| MacIsaac, after Reif F (1995). Understanding Basic Mechanics. Wiley: NY. W180. |
|
|
|
|