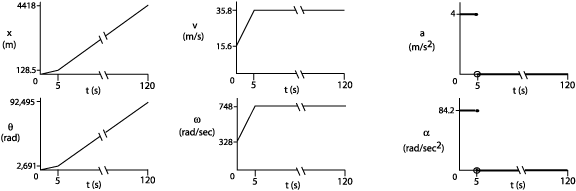
A motorcycle with 0.30 m wheels starts down the highway. It enters the freeway from a ramp at 35mph and smoothly accelerates over 5 seconds to a linear speed of 80 mph. The rider maintains this speed for 2 minutes until he passes a roadside rest stop. Ignore the remainder of this ride, and the part of the trip before the entrance ramp. It may be easiest to do all parts of this question in a different order than stated below.

Q1: Find the linear velocity in m/s of the motorcycle entering the highway and as it passes the rest stop.

Q2: Find the linear acceleration in m/s² during the 5 s acceleration phase of this ride.

V = V_o + at

35.75 m/s = 15.64 m/s + a(5s)

a = 4.02 m/s²

Q3: Use kinematics equations from Chapter 2 to find how far the m/c travels during the first five seconds, the last 2 minutes and for the complete ride described.

1st 5 seconds: x = 1/2(V_o + V)t

x = 1/2(15.64 m/s + 35.75 m/s)5 sec = 128.475 meters

Last 2 minutes: x = 1/2(V_o + V)t

x = 1/2(35.75 m/s + 35.75 m/s)120 sec = 4,290 meters

Complete ride: 128.475 m + 4,290 m = 4,418.475 m

Q4: Find angular velocities of the motorcycle wheels when entering the highway and as the m/c passes the rest stop.

Entering highway:

At rest stop:

Q5: Find the angular acceleration of the m/c wheels during the 5 s acceleration phase of the ride.

w = w_o + at

748.37rad/sec = 327.56rad/sec + a(5sec)

a = 84.24rad/sec²

Q6: Find the number of turns made by the wheels during the first five seconds, the last 2 minutes and for the complete ride described.

q = w_ot + 1/2at²

First five seconds:

q = (327.56rad/sec)(5sec) + 1/2(84.24rad/sec²)(5sec)²

q = 2,690.8 rad

Last two minutes:

q = (748.37rad/sec)(120sec) + 1/2(0)(5sec)²

q = 89,804.4 rad

Complete ride:

2,690.8 rad + 89,804.4 rad = 92,495.2 rad

Q7: Use the relationship between linear and angular rolling motion without slipping to confirm #6 with #3. Comment.

First 5 seconds:   linear (#3): 128.475 m     angular (#6): 2,690.8 rad

Last two minutes:   linear (#3): 4,290 m       angular (#6): 89,804.4 rad

A simple conversion can be employed to show the relationship between linear and angular rolling motion. In this example, it is important to note the size of the wheels being 0.30 meters. With this information, we can say that for every revolution of the wheels, the motorcycle has gone 0.30 m. One revolution of the wheels is equivalent to 2prad. Performing a simple conversion with this information as shown above illustrates the relationship between linear and angular rolling motion.

Q8: Sketch crude graphs of x, v, a vs. t and q, w, a vs. t for this ride. Label the identification points above.