|
|
|
|
| Solution |
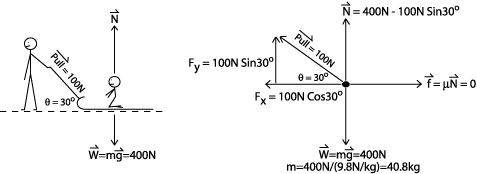
| A girl pulls her little brother on a sled across a frozen lake, and friction is so small you can ignore it. The sled with the boy has a weight of 400 Newtons, and the girl pulls with a force of 100 N at an angle of thirty degrees above the horizontal. |
|
Q1: Draw this situation. Include the weight of the sled, the normal force and the force on the sled due to the girl's pull.
Q2: Calculate the normal force of the ice on the sled. Notice it is not equal to the weight of the sled and the boy. Explain this in your own words. The normal force of the ice on the sled is not equal to the weight of the sled and the boy because the girl is pulling the sled with an upward force equal to 100N Sin30°. To calculate the normal force of the ice on the sled, we must subtract this vertical component of the force that the girl exerts on the sled and the boy from the weight of the sled and the boy. This calculation can be done as follows: Normal force = 400N - 100Nsin30° = 400N - 50N = 350N Q3: Calculate the net force on the sled in the horizontal direction. Calculate the corresponding initial acceleration of the sled. The net force on the sled in the horizontal direction can be determined with trigonometry. Based on the given angle of 30° and the force exerted by the girl, we know that the net force on the sled in the horizontal direction, SFx = 100N Cos30°. To find the corresponding acceleration of the sled, we must employ the equation SFx = max ax = SFx/m m can be found by dividing the weight of the sled and the boy by the force of gravity as follows: m = 400N/(9.8N/kg) = 40.8kg Now, using this information, we can solve for the acceleration of the sled in the x direction: ax = SFx/m = 100N Cos30°/40.8kg = 2.1N/kg or 2.1m/s2 Q4: If the girl can maintain this acceleration for 1.5 seconds, how fast will the sled be moving then? This problem requires us to use the kinematics equation: vf = vo + at We must assume that the initial velocity (vo) of the sled was 0 m/s. vf = 0 m/s + (2.1 m/s2 x 1.5 s) = 0 m/s + 3.2 m/s = 3.2 m/s |
|
|
|
|