Kinematics
2-D Vectors and Coordinate Systems
Solutions

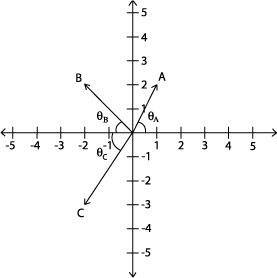
Q1: Draw a Cartesian coordinate system and label the x and y axis. On your coordinate system draw the following three vectors:

A=1x+2y

B=-2x+2y

C= -2x+-3y

Q2: Identify and plot three angles (a,b,c) to describe the direction of each vector.

Q3: Calculate the magnitude and angles of each vector. Mark these on the diagram.

A = 1x + 2y
    magnitude:    c2 = a2 + b2                   c = (a2 + b2)1/2
                        c = (12 + 22)1/2           c = (5)1/2

    angle:   Tanq = 2/1            q = Tan-12              q = 63°

B = -2x + 2y
    magnitude:    c2 = a2 + b2                   c = (a2 + b2)1/2
                        c = (-22 + 22)1/2            c = (8)1/2  

     angle:  Tanq = 2/-2           q = Tan-1-1             q = 45°

C = -2x -3y
    magnitude:    c2 = a2 + b2                   c = (a2 + b2)1/2
                        c = (-22 + -32)1/2            c = (13)1/2

    angle:   Tanq = -3/-2          q = Tan-1-1.5        q = 56°

Q4: Can the x or y component of a vector ever have a greater magnitude then the vector itself? Justify your answer in your own words.

The components of a vector can never have a magnitude greater than the vector itself. This can be seen by using Pythagorean's Thereom.

There is a situation where a component of a vector could have a magnitude that equals the magnitude of the vector. e.g. A=2x + 0y.

Q5: Suppose two vectors have unequal magnitudes. Can their sum ever be zero? Justify your answer in your own words.

No: Magnitude is always positive even if the direction is negative. For the sum of two vectors to equal zero the sum of their respective components must equal zero.

For example:

A = ax + ay B = bx + by

 (ax + ay) + (bx + by) = 0x + 0y

the only way for this to happen is if ax = -bx and ay = -by, but if this were true then using Pythagorean's thereom, the magnitude of A and B would be the same positive value.
Seat Activities
Activity
Contributors