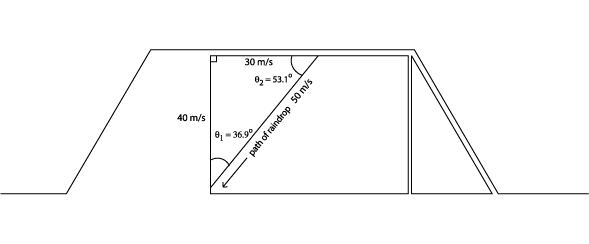
Part 1:

Q1: A car is driving down the highway at 30 m/s. Out of a single thundercloud, a raindrop falls. The raindrop strikes the side window of the car moving directly downward at 40 m/s. It glancingly strikes the glass, skimming from one edge of the glass to the other.

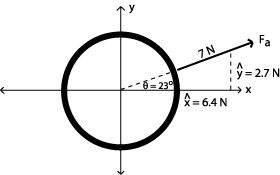
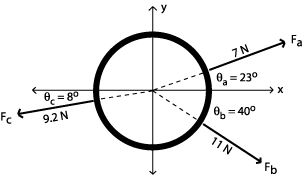
Ignore the effect of drag, gravity and surface tension. Sketch this situation.

Q2: What is the velocity (speed and angle) of the raindrop as it moves across the glass? Describe this mathematically and in your own words.

We know the vertical and horizontal components of the triangle that is formed when the raindrop moves across the window. The vertical component is the velocity of the raindrop, 40 m/s. The horizontal component is the velocity of the car, 30 m/s. Employing the Pythagorean theorem, we can solve for the velocity of the raindrop's path across the window:

c² = a² + b²

c² = (30 m/s)² + (40 m/s)²

c² = 900 m²/s² + 1600 m²/s² = 2500 m²/s²

c = 50 m/s

To find the angle of the path of the raindrop, we must employ a trigonometric function. To solve for q1, we can show:

tan q₁ = (30m/s)/(40m/s), therefore,

q₁ = tan^-1 (30m/s)/(40m/s) = 36.9^o

To solve for q₂, we can show:

tan q₂ = (40m/s)/(30m/s), therefore,

q² = tan^-1 (40m/s)/(30m/s) = 53.1^o

Using this information, we can solve the problem by saying that the raindrop moves across the window at a velocity of 50 m/s, and an angle of 53.1^o below the negative x-axis.

Part 2:

Q1: Determine the magnitude and direction of F_c such that the ring stays stationary. Ignore the force of gravity.

If the ring is to remain stationary, then the sum of all the forces acting on the ring must be equal and opposite. To find a solution to this problem, we must break the forces down into their cartesian components. First, let's deal with F_a.

The force F_a has a magnitude of 7N in a direction 23^o above the positive x-axis. To find the x and y components of this force, we must employ some trigonometric functions. First, to find the y component of F_a we can do as follows:

sin 23^o = y/7N, therefore,

y = 7Nsin23^o = 2.7N

To find the x component of F_a,

cos 23^o = x/7N, therefore,

x = 7Ncos23^o = 6.4 N

Now, let's find the x and y components of F_b:

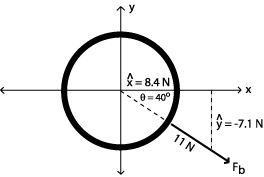
The force F_b has a magnitude of 11N in a direction 40^o below the positive x-axis. To find the x and y components of this force, we must employ some trigonometric functions. First, to find the y component of F_b we can do as follows:

sin 40^o = y/11N, therefore,

y = 11Nsin40^o = -7.1 N

To find the x component of F_b,

cos 40^o = x/11N, therefore,

x = 11Ncos40^o = 8.4 N

Once again, if the ring is to remain stationary, then the sum of all the forces acting on the ring must be equal and opposite. Now we must total the component forces of F_a and F_b. The magnitude of F_c must be equal and opposite to te sum of F_a anf F_b:

F_a: 6.4 N x + 2.7 N y
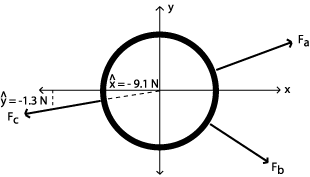
F_b: 8.4 N x - 7.1 N y    (because the y component falls below the x-axis, it is negative!)

F_a + F_b = 6.4 Nx + 2.7 N x + 8.4 Ny - 7.1 N y = 9.1 N x + 1.3 N y

We now know that F_c must have the components: - (9.1 N x + 1.3 N y) = -9.1 N X - 1.3 N y

Using the component information about F_c, we can determine the magnitude of F_c and it's direction:

First, to solve for the magnitude of F_c, we can employ the Pythagorean Theorem as follows:

c² = a² + b²

c² = (-9.1)² + (-1.3)²

c² = 84.5

c = 9.2

So, the magnitude of F_c is 9.2N

To find the direction of the force F_c, we must employ some more trigonometry:

tan q  = -1.3/-9.1 = 0.14

q = tan-1 (0.14) = 8^o

Now we know that the force F_c has a magnitude of 9.2N in a direction 8^o below the negative x-axis.

Q2: Sketch all three forces and describe them in your own words.

The force F_a has a magnitude of 7N in a direction 23^o above the positive x-axis. The force F_b has a magnitude of 11N in a direction 40^o below the positive x-axis. The force F_c has a magnitude of 9.2N in a direction 8^o below the negative x-axis. The ring stays stationary because the sum of all three forces is zero.