1) the charge is moving relative to the magnetic field,
2) the charge's velocity has a component perpendicular to the direction of the magnetic field
 |
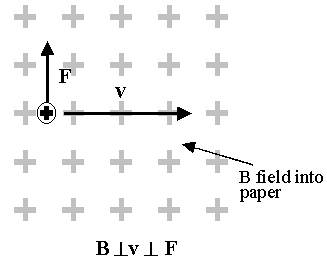
When a charge is placed in a magnetic field, that charge experiences
a magnetic force; when two conditions exist: 1) the charge is moving relative to the magnetic field, 2) the charge's velocity has a component perpendicular to the direction of the magnetic field |
| When using the Right-Hand Rules, it is important to remember that the rules assume charges move in a conventional current (the hypthetical flow of positive charges). In order to apply either Right-Hand Rule to a moving negative charge, the velocity (v) of that charge must be reversed--to represent the analogous conventional current. | 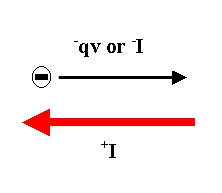 |
 |
Because the force exerted on a moving charge by a magnetic field is perpendicular to both the the velocity of the charge and the direction of the field, making illustrations of these interactions involves using the two symbols on the left to denote movement into or out of the plane of the page. |
Right-Hand Rule #1 determines the
directions of magnetic force, conventional current and the magnetic field.
Given any two of theses, the third can be found.
| Using your right-hand:
point your index finger in the direction of the charge's velocity, v, (recall conventional current). Point your middle finger in the direction of the magnetic field, B. Your thumb now points in the direction of the magnetic force, Fmagnetic. |
Right-Hand Rule #2 (RHR #2)
Right-Hand Rule #2 determines the direction of the magnetic
field around a current-carrying wire and vice-versa
| Using your right-hand:
Curl your fingers into a half-circle around the wire, they point in the direction of the magnetic field, B Point your thumb in the direction of the conventional current.
|
The Right-Hand Rules give only the direction of the magnetic field.
In order to determine the strength of a magnetic field , some useful mathematical
equations can be applied.
| For a long, straight wire, the magnetic field, B is:
mo = 4p x 10-7 T · m / A and os called the permeability of free space, r is the radial distance from the wire in meters, and I is the current in amperes. |
| For a single loop of wire, the magnetic field, B
through the center of the loop is:
mo is the permeability of free space, and R is the radius of the the circular loop of wire, measured in meters. Both the fields for a coil of wire and a solenoid can be constructed from this equation. |
| 2. Here, a long, straight wire carries a current, I, of 3.0 A. A particle, q with a charge of +6.5 x 10-6 C, moves parallel to the wire in the direction shown, at a distance of r = 0.050 m and a speed of v = 280 m / s. Determine the magnitude and direction of the magnetic field experienced by the charge. |
This page contributed to by Camilo Tafur and Dan MacIssac