e2125s.htm

Experiment E2125 Conservation of Angular Momentum

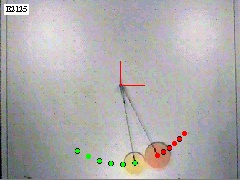
Figure 1. Two pucks have a rotational collision on an air table.

Discussion

Figure 1 shows a picture of two pucks on an air table. The two pucks interact (collide) while following a circular path. During the interaction (collision), the large puck applies a force on the small puck and the small puck applies a force on the large puck. These are action-reaction pairs.

Since the objects are not following linear paths, it is useful to choose a different coordinate system. Figure 2 shows a mass following a circular path. On the left, a coordinate system is shown with t indicating a direction tangent to the path and r indicating a direction perpendicular to the path along the radial line. A free body diagram is shown on the right, where a force other than the tension is applied to the mass. This force is broken into components along the path F_t and perpendicular to the path F_r.

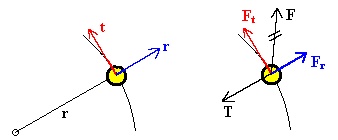
Figure 2. A mass follows a circular path. The tangential force (F_t) will cause a tangential acceleration along the path (a_t).

Analyzing the free body diagram in the radial direction we have:

F_netr = ma_r or T - F_r = mv_t²/r

This is the same result as uniform circular motion. Here, v_t is used to note that v has a direction tangent to the path. Now, since there is a tangential force F_t, there will be a tangential acceleration a_t and v_t will not remain constant. Analyzing the free body diagram in the tangential direction we have:

F_nett = ma_t or F_t = ma_t

Here, the tangential force causes the mass to accelerate in the tangential direction. With this motion, it is easier to work with rotational equations. Table 1 shows the relationships between linear and rotational motions. While you have seen q and w in the section on Uniform Circular Motion, a, I, L, and t are new to this experiment. They are discussed below.

Table 1. A list of relationships between linear and rotational motions. Angles must be measured in radians. The subscript t means tangent to the path or perpendicular (^) to the radial lines.

Linear	Rotational	Relationship
Ds	Dq	Ds = rDq
v_t = Ds/Dt	w = Dq/Dt	v_t = rw
a_t = Dv_t/Dt	a = Dw/Dt	a_t = ra
m	I	I = Sm_ir_i²
p_t = mv_t	L = Iw	L = rp_t
F_t = ma_t	t = Ia	t = rF_t

Angular Acceleration

Angular acceleration is defined as the change in angular velocity with respect to time.

a = Dw/Dt

Notice that the angular acceleration is the slope of an angular velocity versus time graph. The SI units for angular acceleration are 1/s².

Rotational Inertia

Rotational inertia, I, depends on the object's mass and how the mass is distributed from the axis of rotation. In general, if the object is broken into small masses m_i, each at a radius r_i from the axis of rotation, then we define I as:

I = Sm_ir_i²

Here, m is the mass in kg and r is the radius of the circular path in meters. The SI units of rotational inertia are kg^.m².

Angular Momentum

Angular momentum, L, is the product of the object's rotational inertia and its angular velocity.

L = Iw

Here, I is the rotational inertia and w is the angular velocity. The SI units of angular momentum are kg^.m²/s.

In Table 1, the relationship between L and p is written:

L = rp_t

This means that the magnitude of L equals the magnitude of r multiplied by the magnitude of the momentum tangent to the path. We can also say that the magnitude of L equals the magnitude of r multiplied by that part of the momentum that is perpendicular to the radial line. This is written:

L = r_^p

Torque

The net torque, t, acting on an object is the slope of its angular momentum versus time graph.

t_net = DL/Dt

The SI units of torque are kg^.m²/s² or N^.m.

If the object's rotational inertia doesn't change, then the net torque is also the product of the object's rotational inertia and its angular acceleration.

t_net = Ia

In Table 1, the relationship between t and F is written:

t = rF_t

This means that the magnitude of t equals the magnitude of r multiplied by the magnitude of the force tangent to the path. We can also say that the magnitude of t equals the magnitude of r multiplied by that part of the force that is perpendicular to the radial line. This is written:

t = r_^F

Return to Top

The Model

Newton's Third Law Revisited

Newton's third law says that if one object exerts a force on a second object, then the second object exerts an equal but oppositely directed force on the first object. This is shown for two pucks in the left drawing of Figure 3 where F₁₂ = - F₂₁.

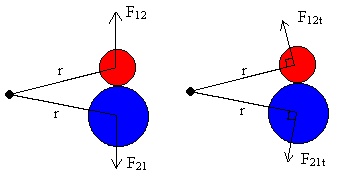
Figure 3. The diagram on the left shows the contact forces on the two pucks during the collision. On the right only the components of the forces that are perpendicular to the radial arms are shown. Tensions and the components of the contact forces parallel to the radial arms are not shown. These forces would combine in the radial direction and have no effect on the motion along the circular path.

Examining Figure 3, and realizing that F₁₂ = - F₂₁ from Newton's third law, we see that:

rF_12t = - rF_21t or r_^F₁₂ = - r_^F₂₁

Here, ^ means we use the perpendicular components of the radial arm and the force. However, these are torques (see Table 1 in the Discussion section), so we can write:

t₁₂ = -t₂₁

Now torque is the slope of an angular momentum versus time graph so we can write:

DL₁/Dt = -DL₂/Dt

This says that when the objects are interacting, the slope of object 1's angular momentum versus time graph is the negative slope of object 2's angular momentum versus time graph. You can check the validity of this equation, and Newton's Third Law, by finding the slopes of the angular momentum versus time graphs.

If the above equation is valid, then:

DL₁ = -DL₂

This is true since the objects interact for the same amount of time. This says that the loss in angular momentum of one object equals the gain in angular momentum of the other object. Expanding we get:

L_1f - L_1i = -(L_2f - L_2i)

Here, the subscripts i and f mean initial and final respectively. Rearranging we have:

L_1f + L_2f = L_1i + L_2i

And finally:

L_Tf = L_Ti

Here, the subscript T means total.

If the above mathematical argument is physically valid, then we can make a statement about the total angular moment under certain conditions.

Conservation of Angular Momentum

If the only important torques acting on two colliding objects are internal torques, then the objects' total angular momentum is conserved.

Rotational Inertia

In this experiment, the mass is an air table puck. The puck travels in a circle with radius, r. Since the radius of the puck is small compared to the radius of the circular path, we can treat the puck as a point mass. Then the rotational inertia is:

I = mr²

You should check the values for the rotational inertias in the computer. The values can be changed with the Mass 1 and Mass 2 buttons if they are not correct.

Return to Top

Marking the Video

Click here to open the video.

Play the video and observe the motion.
Select the Video Scale menu item, then the New Origin sub item. Place the new origin at the axis of rotation.
Mark the orange puck until the video does not step any more.
Click the Data Set 1 button and you will see its caption change to Data Set 2. Mark the yellow puck until the video does not step any more. These marks will be shown as green circles.
When you move the mouse on the video, notice the x and y positions changing below the video. Move the mouse to the new origin and you will see that both x and y are zero. Move the mouse to a point on the circular path and find the radius of the motion.
Press the Mass1 button and you will see a window showing both the mass and rotational inertia of object 1. Calculate the rotational inertia using the mass and the radius. Is the rotational inertia correct in the computer? If so, press the cancel button to keep the values. Check object 2's rotational inertia using the Mass2 button.

Return to Top

Graphical Analysis

Press the GRAPHS Button and the Data Analysis Choices will appear. Pick Option 10. Click the Next button.
Select Angular Velocity and Angular Momentum plots. Click the Next button.
Observe the angular velocity graph. There are three plots shown, w₁, w₂ and w, where w is the sum of w₁ and w₂. Is w conserved? Does the model say it should be conserved?
Find the slope of each object's w versus time plot. What is the physical meaning of these slopes? Are these two slopes the negatives of one another? Does the model say they should be?
Observe the angular momentum graph. There are three plots shown, L₁, L₂ and L, where L is the sum of L₁ and L₂. Is L conserved? Does the model say it should be conserved?
Find the slope of each object's L versus time plot. What is the physical meaning of these slopes? Are these two slopes the negatives of one another? Does the model say they should be?