


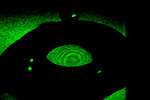
In the traditional version of Newton's Rings, a slightly convex lens is placed above a flat glass plate or optical flat.
Monochromatic light is used to illuminate the lenses. This can be produced by any laser. Frosted plastic is placed in front of the laser to diffuse the light.
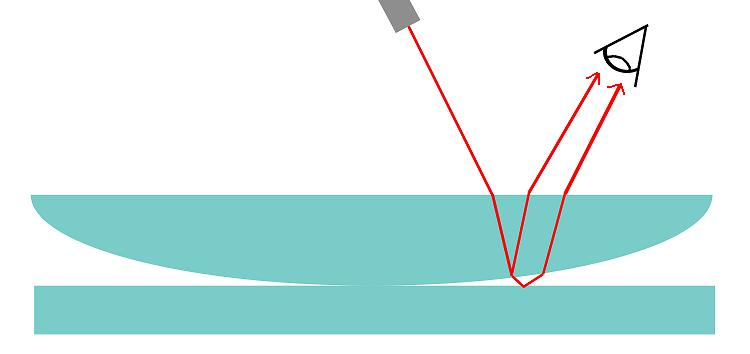
The light goes through the convex lens. There is a small pocket of air between the convex lens and the flat lens. Some of the light will reflect at this barrier. The rest of the light will refract in accordance to Snell's Law.
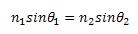
| Variable | Name |
| n | index of refraction |
| θ | angle between light and normal |
The refracted light reflects off of the flat lens. These two beams of light will be at different points. Because the light goes through the lens at multiple places, the reflected light will interfere both constructively and deconstructively. This is what causes the dark and bright fringes.
For more information on Snell's Law, see the information here and interference here.
The radius of the rings can be found with the following equation:
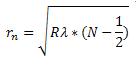
| Variable | Meaning |
| rn | radius of ring from center |
| R | radius of curvature of lense |
| N | ring number observed |
| λ | wavelength of light |
Alternatively, the radius of curvature could be found:
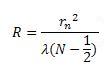
Microscope slides are a variation on this concept. Instead of a convex lens over a flat lens, there are two lenses at an angle to each other. This can be achieved by placing a piece of hair or a piece paper at the edge of the two slides. This will create an air wedge between the two lenses.
As with the convex lens, the light will reflect at different angles. However, they will appear as partial rings since the compressed spot is at one edge instead of the center.
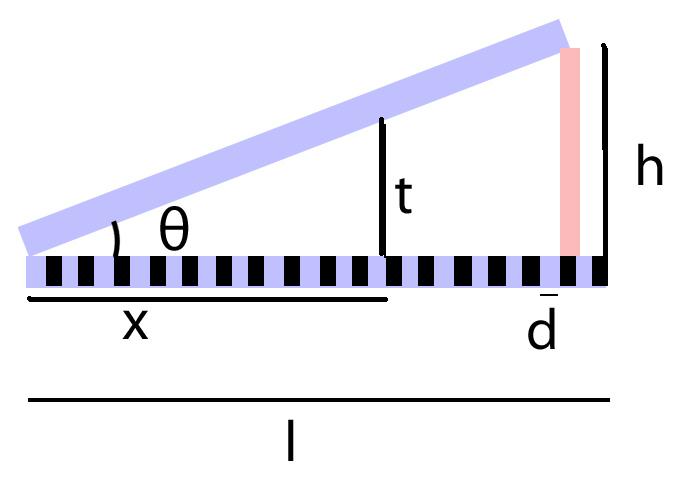
| Variable | Meaning |
| n | dark fringe looked at |
| x | distance to fringe |
| l | total distance |
| t | height at n |
| h | total height |
| d | distance between dark fringes |
| λ | wavelength of light |
| θ | Angle |
There are three main equations for the above diagram:
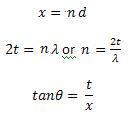
From this, a more easily solvable equation can be derived.
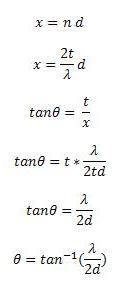
This allows for the angle to be found, using the wavelength of light, and the distance between fringes.
Microscope slides do not necessarily need hair or paper to form a wedge. This is because the slides are random, and they will not rest completely flat against the other, and this will create pockets of air. However, this leads to less predictable patterns, but the above equations can be used to approximate the angles created by the slides' imperfections.