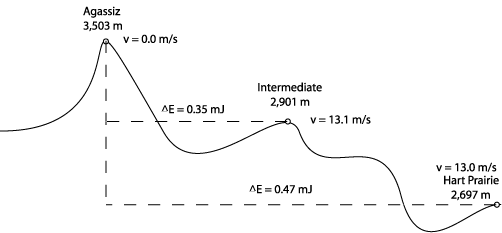
Q1: What is the skier's speed at the intermediate point?

Using the conservation of momentum, we have the formulas;

W_nc = E_f - E_{o  and}  W_nc = (1/2mv_f² + mgh_f) - (1/2mv_o² + mgh_o)

Using the given information, it is stated that the skier starts from rest at the highest point. The initial velocity (V_o) is zero and solving for the final velocity (V_f) we get:

V_f = [2(W_nc +mg(h_o - h_f))/m]^1/2

Wnc = -400 kJ + 50 kJ = -350 kJ (-350,000 J)  m = 60.0 kg,  g = 9.8 m/s2, h_f = 2,901 m, h_o = 3,505 m

V_f = [2({-350,000 J} + {60.0 kg}{9.8m/s²}(3,505 m - 2,901 m))/ {60.0 kg}]^1/2

V_f = 13.1 m/s

Q2: What is the skier's final velocity (V_f) at the foot of the Hart Prairie run?

W_nc = -400 kJ - 170 kJ + 50 kJ + 50 kJ = -470 kJ m = 60.0 kg, g = 9.8 m/s², h_f = 2,697 m, h_o = 3,505 m

V_f = [2({-470 kJ} + {60.0 kg}{9.8m/s2}(3,505 m - 2,697 m))/{60.0 kg}]^1/2

Using the same formulas from the previous equation with a larger W_nc and a lower h_f, we end up with 13.0 m/s for V_f.

Q3: Please draw a crude sketch calculating Kinetic energy (KE), Gravitational potential energy (GPE), and total energy at the three points labeled Agassiz (start), Intermediate, and Hart Prairie (final). Use SI (m, k, and s) units throughout. Remember: [1.0 m = 3.281 ft]

KE = 1/2mv², GPE = mgh, TE = 1/2mv²+ mgh

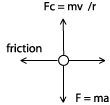
Advanced Question: Near the very foot of Hart Prairie run there is a small circular 'speed bump' hill of radius 5.0 m. At what minimum V_f will the skier become airborne? Does this particular skier become airborne? (Draw a FBD)